

 新聞資訊
新聞資訊 知識專欄
知識專欄基于回旋共振的實驗技術用于測量半導體中載流子的有效質量,但在金屬中效果不佳。在本教程中,我們將研究一些俄羅斯物理學家測試的類似技術。
費米表面
在前一期中,我們看到在Sommerfeld模型中,金屬的導電電子的能量ε接近費米能量εF。由于這是一個半經典模型,因此引用費米速度vF和相對軌跡(規避海森堡不確定性原理)是合理的。換句話說,在上述模型中,量子效應融入了費米-狄拉克統計分布,而不是單個電子的動力學。因此,該模型被稱為半經典模型。
我們將e表示為動量(或沖量)p = mev 的函數:

從中,可以唯一定義費米沖量:

下一步是應用德布羅意假設(舊量子理論):與電子相關的物質波是一個平面波,其傳播向量為:

方程(1)變為:
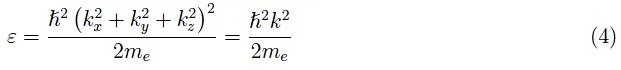
這又將單個電子的能量表示為德布羅意波的傳播向量的笛卡爾分量的函數。因此,我們得到一個包含三個實變量的實函數,其圖形位于R4中(無法可視化)。然而,我們可以描繪上述函數的等能量面,這些面稱為等能面。更精確地說,如果ε0是允許的能量值,則相應的等能面為:
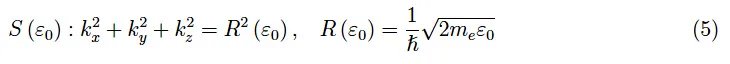
也就是說,這是一個以k空間原點為中心的球體(三維歐幾里得空間),半徑為R(ε0)。特別地,費米球是表面S(εF)。具有量子知識的讀者會將波數k = |k|視為“良好的量子數”,因為k唯一定義了單個電子的量子態,專門參考統計分布,而忽略自旋。ε的唯一定義源于對k的函數依賴性,如方程(4)所表達。
由于在k空間中,能量ε的分布是各向同性的,因而e通過其模與k相關,因此相應的等能面(球體)上的點代表物理上不同的狀態,但具有相同的能量。在量子力學中,這通過聲稱能級ε是簡并的,并且具有無限的簡并度來表達。更精確地說,即等于上述表面的點數。然而,我們必須考慮自旋的自由度。一般來說,由自旋引起的簡并度寫為gs = 2s + 1,其中s是所考慮粒子的自旋。在電子的情況下,s = 1/2,因此gs = 2;實際上,任何自旋為1/2的狀態k(即被自旋向上的電子占據)與波數k相同但自旋為1/2(自旋向下)的狀態是不同的。
這兩種狀態具有相同的能量;因此,額外的簡并度等于2。注意,泡利不相容原理并沒有被違反,因為上述狀態在物理上是不同的。而且,由于它們是無限多的,每個狀態占據著一對自旋向上和向下的電子,因此可以考慮與所考慮的晶體的理論無限延展相兼容的幾乎無限數量的電子(以不破壞晶格的周期性)。
根據Sommerfeld模型,貢獻于金屬電導率的電子是那些在k空間的費米球上“分配”的狀態。此狀態的分布是各向同性的,因此對于替換k -> -k是對稱的。由于k通過方程(3)與單個電子的動量p相關,整體動量為零,因此電流流動(電流密度)也為零。施加均勻的靜電場E,轉化為作用在單個電子上的恒定力F = eE。
根據動量定理,電子動量隨時間的變化δt為δp = Fδt,這對應于方程(3)中的δk。因此,電場的作用是將費米球在k空間中平移。這破壞了各向同性,因此也破壞了k和-k之間的對稱性。結果是非零的總動量,因此電荷的凈流動。電場瞬時關閉將重建初始配置(沒有電流),將費米球的中心移動到k空間坐標系的原點。這是通過涉及電子-晶格碰撞的統計機制幾乎瞬時發生的。
金屬中的回旋共振
在之前的教程中,我們看到在半導體中,測量由于施加均勻的磁靜場B0而引起的回旋頻率ωc是通過測量沿B0傳播的平坦單色電磁波的吸收來實現的。在金屬的情況下,由于以下原因,這種技術難以實施:
除非使用頻率ω > ωp(其中ωp是與導電電子密度n成正比的等離子頻率),否則金屬幾乎完全反射電磁波。由于金屬的n大約是1023 cm?3,因此ωp的數量級約為1016 rad/s,對應的頻率fp約為104 GHz。
頻率ω > ωp的電磁波的穿透深度δ相對較低(皮膚效應)。頻率f = 1 GHz時,δ的典型值約為10?5 cm;δ在給定金屬中定義了所謂的皮膚區域。
如前所述,在大多數金屬中,費米表面并不是球形的。這破壞了單個電子能量分布相對于k的各向同性。因此,通過改變B0的方向,可以得到不同的回旋頻率。
一些俄羅斯物理學家測試的技術包括使用一個金屬板,施加與板平面平行的磁場B0。通過這種方式,單個電子的軌跡軸包含在上述平面內。
注:此技術的變體是由Azbel-Kaner幾何提供的。
射頻場垂直于B0發送。如果R0 > δ(其中R0是單個回旋軌道的半徑),那么只有一部分軌道將受到電磁場的作用。然而,穿越皮膚區域的電子可以從電磁場吸收能量,從而加速。在相反的情況下(即如果它向電場釋放能量),它會減速。在回旋加速器(粒子加速器)中會發生類似的機制;因此,電磁學文獻中稱ωc為“回旋頻率”,也稱為拉莫爾頻率。
因此,我們期望吸收峰(共振),但是在電子向射頻場釋放能量的情況下也是如此。具體來說,電子在與B0垂直的平面上的周期性運動的投影必須與電磁場同相位。如果Tc = 2π/ωc是上述運動的周期,T = 2π/ω是電磁場的周期,則必須滿足Tc = nT,其中n是正整數。回憶回旋頻率ωc的表達式,我們得到共振條件:

此條件返回磁靜場B0的值,其中電子與射頻場處于共振狀態。在堿金屬的情況下,費米表面大約是球形的,針對不同的n > 1值測量B0的值,從而通過方程(6)獲得有效質量,然后對獲得的結果進行平均。對于在氦溫度下的銅,見參考文獻。
結論
回旋共振實驗不僅可以測定金屬和半導體中載流子的有效質量,還為研究費米表面的拓撲提供了極好的工具。
浮思特科技專注功率器件領域,為客戶提供IGBT、IPM模塊等功率器件以及MCU和觸控芯片,是一家擁有核心技術的電子元器件供應商和解決方案商。